Francis Galton as Statistician
Galton was able to place his researches about heredity on a scientific basis by applying novel statistical concepts, and can justly be claimed as one of the very first social scientists, if not the first. This would pave the way for the development of statistics as a discipline, through Galton's follower Karl Pearson. It would also lay the foundation for the study of differential psychology: through Charles Spearman, who was heavily influenced by Galton and made important contributions of his own to the development of factor analysis; and through Cyril Burt and his pupils, who moulded the study of intelligence and hereditary ability into a formidable discipline. There are few aspects of modern social science that do not (or at least, should not) rely on the statistical innovations that Galton introduced.
Ironically, Galton was not himself a mathematician, though he was competent enough, but really an intensely practical man. He left the refinement of his techniques to dedicated and supremely talented mathematicians like Pearson, but provided the crucial formation of concepts; he was a practical innovator, not a technician. Galton first discovered regression, which he initially called reversion, by experimenting with sweet peas. His sweet peas produced seeds with a (normal) variation of sizes that regressed from the distribution of their parents.
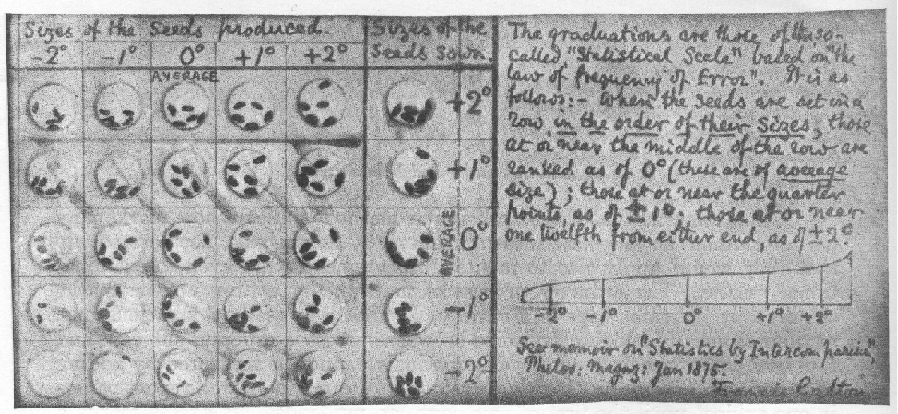
Some years later, he formulated the statistical correlation coefficient by another indirect route, painstakingly graphing and re-graphing his data about bivariate normal distributions until he realized that the formulae for elliptical curves (a topic popular in 19th century mathematics but almost entirely moribund today) could provide him with a method for summarizing with a number the graphical relationship he saw. This number could then be used to reason about the relationship, and form a basis for comparisons. Following the suggestion of a friend, he approached a Cambridge mathematician to work out the details for him - an approach he was able to pursue very fruitfully in later years with Pearson.
| Facsimile | 1874 | On a proposed statistical scale. [Letter] | Nature 9 (March 5) : 342-3 |
| Facsimile | 1875 | 'Statistics by intercomparison with remarks on the Law of Frequency of Error.' | Philosophical Magazine 49 : 33--46 |
| Facsimile | 1877 | 'Considerations adverse to the maintenance of Section F.' | Journal of the Statistical Society 40 (September) : 468-73 |
| Facsimile | 1879 | 'The geometric mean, in vital and social statistics.' | Proceedings of the Royal Society 29 (November 20) : 365-7 |
| Facsimile | 1885 | 'Anthropometric percentiles.' | Nature 31 : 223-5 |
| Facsimile | 1888 | 'Co-relations and their measurement, chiefly from anthropometric data.' | Proceedings of the Royal Society 45 (December 13) : 135-45 |
| Facsimile | 1889 | 'Correlations and their measurement, chiefly from anthropometric data.' | Nature 39 : 238 |
| Facsimile | 1890 | 'Kinship and Correlation' | North American Review 150 : 419-431 |
| Facsimile | 1890 | 'Dice for statistical experiments.' | Nature 42 : 13-4 |
| Facsimile | 1892 | Notes to George K. Holmes on the Subject of Distribution | Publications of the American Statistical Association : 271-3 |
| Facsimile | 1894 | 'Note on fitting normal curves to distribution of speeds of old homing pigeons' | Homing News and Pigeon Fanciers' Journal (April 6) : 159-60 |
| Facsimile | 1894 | 'A plausible paradox in chances.' | Nature 49 : 365-6 |
| Facsimile | 1895 | 'A new step in statistical science.' [Letter] | Nature 51 : 319 |
| Facsimile | 1896 | "Application of the Method of Percentiles to Mr. Yule's Data from the Distribution of Pauperism". | Journal of the Royal Statistical Society 59 : 392-396 |
| Facsimile | 1897 | 'Note to the memoir by Professor Karl Pearson, F.R.S., on spurious correlation.' | Proceedings of the Royal Society 60 (February 18) : 498-502 |
| Facsimile | 1899 | 'The median estimate.' | Report of the British Association for the Advancement of Science 69 : 638-40 |
| Facsimile | 1899 | 'The median estimate.' | Nature 60 : 584 |
| Facsimile | 1899 | 'A geometric determination of the median value of a system of normal variants from two of its centiles.' | Nature 61 : 102-4 |
| Facsimile | 1902 | 'The most suitable proportion between the values of first and second prizes.' | Biometrika 1 : 380-90 |
| Facsimile | 1907 | 'Grades and deviates.' | Biometrika 5 : 400-4 |
Galton has left an excellent description of his discovery of correlation and regression, in an article he published for the North American Review in 1890, "Kinship and Correlation". Some idea of Galton's influence on statistics can also be gained from the following obituary, which appeared in the Journal of the Royal Statistical Society.