APPENDIX C. 225 ,
C.
EXPERIMENTS ON SWEET PEAS BEARING ON THE LAW OF REGRESSION.
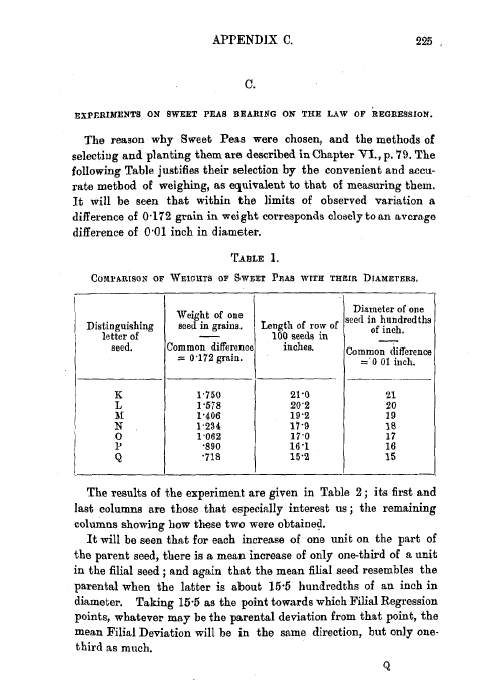
The reason why Sweet Peas were chosen, and the methods of selecting and planting them are described in Chapter VI., p. 79. The following Table justifies their selection by the convenient and accurate method of weighing, as equivalent to that of measuring them. It will be seen that within the limits of observed variation a difference of 0.172 grain in weight corresponds closely to an average difference of 0.01 inch in diameter.
TABLE 1.
COMPARISON OF WEIGHTS OF SWEET PEAS WITH THEIR DIAMETERS.
| |
Weight of one |
|
Diameter of one |
|
Distinguishing |
seed in grains. |
Length of row of |
seed io hundredths |
|
letter of |
|
100 seeds in |
of inch. |
|
seed. |
Common difference |
inches. |
Common difference |
| |
= 0.172 grain. |
|
='O 01 inch. |
|
K |
1.750 |
21'0 |
21 |
|
L |
1.578 |
20'2 |
20 |
|
it |
1.406 |
19'2 |
19 |
|
N |
1.234 |
17'9 |
18 |
|
0 |
1062 |
17'0 |
17 |
|
P |
890 |
16.1 |
16 |
|
Q |
718 |
15.2 |
15 |
The results of the experiment are given in Table 2 ; its first and last columns are those that especially interest us ; the remaining columns showing bow these two were obtained.
It will be seen that for each increase of one unit on the part of the parent seed, there is a mean increase of only one-third of a unit in the filial seed ; and again that the mean filial seed resembles the parental when the latter is about 1.5.5 hundredths of an inch in diameter. Taking 15'5 as the point towards which Filial Regression points, whatever may be the parental deviation from that point, the mean Filial Deviation will be in the same direction, but only onethird as much.