vii.) DISCUSSION OF THE DATA OF STATURE. 109
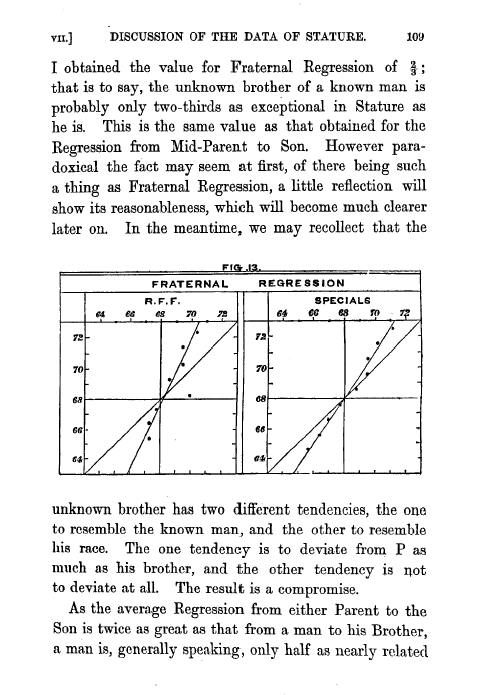
I obtained the value for Fraternal Regression of 2 ; that is to say, the unknown brother of a known man is probably only two-thirds as exceptional in Stature as he is. This is the same value as that obtained for the Regression from Mid-Parent to Son. However paradoxical the fact may seem at first, of there being such a thing as Fraternal Regression, a little reflection will show its reasonableness, which will become much clearer
later on. In the meantime, we may recollect that the
|
FRATERNAL REGRESSION |
|
| |
R. F. F.
94 ed as 70 7E |
|
|
|
|
72 |
|
|
|
|
|
|
70 |
|
|
|
|
|
|
68 |
|
|
|
|
|
| |
|
| |
|
|
go
64 |
AiA |
|
|
FA* |
|
| |
|
|
|
|
|
unknown brother has two different tendencies, the one to resemble the known man, and the other to resemble his race. The one tendency is to deviate from P as much as his brother, and the other tendency is not to deviate at all. The result is a compromise.
As the average Regression from either Parent to the Son is twice as great as that from a man to his Brother, a man is, generally speaking, only half as nearly related