vii.)   DISCUSSION OF THE DATA OF STATURE.   109

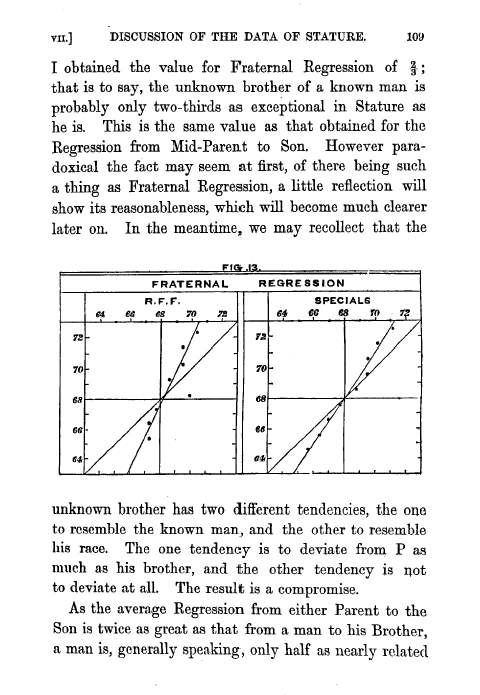
I obtained the value for Fraternal Regression of 2 ; that is to say, the unknown brother of a known man is probably only two-thirds as exceptional in Stature as he is. This is the same value as that obtained for the Regression from Mid-Parent to Son. However paradoxical the fact may seem at first, of there being such a thing as Fraternal Regression, a little reflection will show its reasonableness, which will become much clearer

later on. In the meantime, we may recollect that the

unknown brother has two different tendencies, the one to resemble the known man, and the other to resemble his race. The one tendency is to deviate from P as much as his brother, and the other tendency is not to deviate at all. The result is a compromise.

As the average Regression from either Parent to the Son is twice as great as that from a man to his Brother, a man is, generally speaking, only half as nearly related